机器学习之朴素贝叶斯详解
目录
朴素贝叶斯概述
朴素贝叶斯(Naive Bayes)是一种基于贝叶斯定理的概率分类算法,属于监督学习中的生成模型。它以其简单、高效和在某些场景下的优秀表现而闻名。
核心思想
朴素贝叶斯的核心假设是特征条件独立性,即假设所有特征之间相互独立。虽然这个假设在现实中往往不成立,但正是这种”朴素”的假设使得算法计算简单且效果良好。
分类原理
利用贝叶斯公式根据特征的先验概率计算出其后验概率,然后选择具有最大后验概率的类作为该特征所属的类:
$$P(C|X) = \frac{P(X|C) \cdot P(C)}{P(X)}$$
其中:
- $P(C|X)$ 是后验概率
- $P(X|C)$ 是似然概率
- $P(C)$ 是先验概率
- $P(X)$ 是证据因子
数学基础
条件概率
条件概率是指在事件B发生的情况下,事件A发生的概率,记作 $P(A|B)$:
$$P(A|B) = \frac{P(A \cap B)}{P(B)}$$
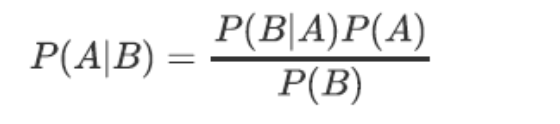
全概率公式
如果事件 $A_1, A_2, …, A_n$ 构成一个完备事件组且都有正概率,那么对于任意事件B:
$$P(B) = \sum_{i=1}^{n} P(B|A_i) \cdot P(A_i)$$
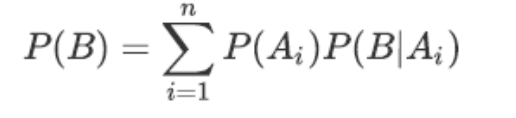
贝叶斯公式
根据条件概率和全概率公式,可以得到贝叶斯公式:
$$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$$
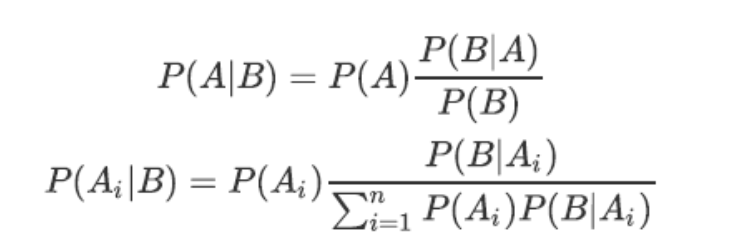
贝叶斯公式的组成部分
- 先验概率 $P(A)$:在B事件发生之前,对A事件概率的判断
- 后验概率 $P(A|B)$:在B事件发生之后,对A事件概率的重新评估
- 似然函数 $P(B|A)$:在A发生的条件下,B发生的概率
- 调整因子 $\frac{P(B|A)}{P(B)}$:使得预估概率更接近真实概率
调整因子的作用
- 调整因子 > 1:事件B发生时,事件A发生的可能性变大,先验概率被增强
- 调整因子 = 1:事件B无助于判断事件A的可能性
- 调整因子 < 1:事件B发生时,事件A发生的可能性变小,先验概率被削弱
分类任务的贝叶斯表达式
对于分类问题,我们需要找到使得 $P(C_i|X)$ 最大的类别 $C_i$:
$$C_{pred} = \arg\max_{C_i} P(C_i|X) = \arg\max_{C_i} \frac{P(X|C_i) \cdot P(C_i)}{P(X)}$$
由于 $P(X)$ 对所有类别都相同,可以简化为:
$$C_{pred} = \arg\max_{C_i} P(X|C_i) \cdot P(C_i)$$
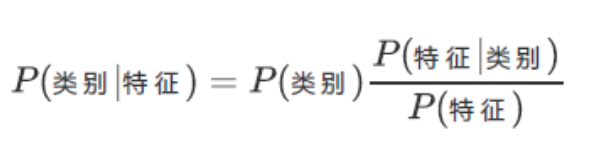
朴素贝叶斯分类器
朴素贝叶斯有三种主要变体,分别适用于不同类型的数据:
1. 高斯朴素贝叶斯 (GaussianNB)
适用于连续型特征,假设特征服从正态分布。
数学原理
对于连续特征 $x_j$,假设其服从正态分布:
$$P(x_j|C_i) = \frac{1}{\sqrt{2\pi\sigma_{ij}^2}} \exp\left(-\frac{(x_j - \mu_{ij})^2}{2\sigma_{ij}^2}\right)$$
其中 $\mu_{ij}$ 和 $\sigma_{ij}^2$ 分别是类别 $C_i$ 下特征 $x_j$ 的均值和方差。

代码示例
1 | from sklearn.naive_bayes import GaussianNB |
2. 多项式朴素贝叶斯 (MultinomialNB)
适用于离散型特征,特别是文本分类中的词频统计。
数学原理
假设特征服从多项式分布:
$$P(x_j|C_i) = \frac{N_{ij} + \alpha}{N_i + \alpha \cdot n}$$
其中:
- $N_{ij}$ 是类别 $C_i$ 中特征 $x_j$ 出现的次数
- $N_i$ 是类别 $C_i$ 中所有特征的总次数
- $\alpha$ 是平滑参数(通常为1)
- $n$ 是特征总数

代码示例
1 | from sklearn.naive_bayes import MultinomialNB |
3. 伯努利朴素贝叶斯 (BernoulliNB)
适用于二值特征,如文本分类中的词是否出现。
数学原理
假设特征服从伯努利分布:
$$P(x_j|C_i) = p_{ij}^{x_j} \cdot (1-p_{ij})^{1-x_j}$$
其中 $p_{ij}$ 是类别 $C_i$ 中特征 $x_j$ 为1的概率。

代码示例
1 | from sklearn.naive_bayes import BernoulliNB |
实际应用
文本分类
朴素贝叶斯在文本分类中表现优异,特别是垃圾邮件检测:
1 | import pandas as pd |
情感分析
1 | # 情感分析示例 |
医疗诊断
1 | import numpy as np |
优缺点分析
优点
- 简单高效:算法简单,训练和预测速度快
- 小样本效果好:在小数据集上表现良好
- 处理多分类问题:天然支持多分类
- 处理缺失值:对缺失值不敏感
- 增量学习:支持在线学习
缺点
- 特征独立性假设:现实中特征往往相关
- 对输入数据敏感:需要良好的特征工程
- 概率估计问题:可能出现零概率问题
- 特征重要性:无法直接评估特征重要性
适用场景
- 文本分类(垃圾邮件检测、情感分析)
- 医疗诊断
- 推荐系统
- 金融风险评估
- 图像分类(简单场景)
总结
朴素贝叶斯是一种经典而实用的机器学习算法,虽然基于”朴素”的独立性假设,但在许多实际应用中表现优异。它的主要优势在于:
- 理论基础扎实:基于贝叶斯定理,有坚实的数学基础
- 实现简单:算法逻辑清晰,易于理解和实现
- 效果可靠:在文本分类等任务中表现突出
- 计算效率高:训练和预测速度都很快
选择合适的朴素贝叶斯变体(高斯、多项式或伯努利)取决于数据的特征类型,而良好的特征工程和适当的平滑处理是提高模型性能的关键。
参考资料:
- CSDN博客:朴素贝叶斯详解
- Scikit-learn官方文档
- 《机器学习》周志华著