Nginx详解
Nginx详解与部署流程在项目初期,如果并发量较小,用户数量有限,通常只需通过一个jar包启动应用,内部由自带的Tomcat处理请求即可满足需求。但随着用户量和并发量的提升,单一应用实例可能无法承载全部流量,这时就需要引入Nginx进行负载均衡和反向代理,提升系统的可用性和扩展性。 为什么选择NginxNginx(engine...
大模型学习之MCP
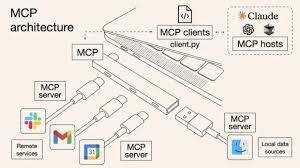
MCP视频链接 RAG 技术的局限性RAG(检索增强生成,Retrieval-Augmented Generation)是当前大模型领域的热门方向。它结合了信息检索与生成式模型,旨在提升知识准确性、上下文理解和对最新信息的利用能力。 RAG 的主要缺点: 检索精度有限,可能无法获取最相关的信息 生成内容可能不完整或片面 缺乏全局视角 检索能力受限时效果下降 理论基础Function CallFunction Call 是 OpenAI 于 2023 年提出的重要概念,本质上为大模型提供了与外部系统交互的能力,相当于为模型配备“外挂工具箱”。当模型无法直接回答问题时,可主动调用预设函数(如查询天气、计算数据、访问数据库等),获取实时且精准的信息后再生成回答。 Model Context Protocol(MCP)MCP(模型上下文协议)由 Anthropic 公司提出,是一个开放标准协议,旨在解决 AI 模型与外部数据源、工具的交互难题。 开发者按照 MCP 协议开发,无需为每个模型与不同资源重复编写适配代码,大幅节省开发工作量。MCP Server...
Docker部署python项目
Docker部署python项目目的:为了解决生产环境和开发环境的环境版本问题,同时也是因为不同服务器中的git库同步不方便的原因所以使用docker进行开发部署。 最终结论是选择拉取基础镜像直接在镜像中进行开发最为方便 开发部署流程 方式一:直接在docker容器中开发 操作:启动一个基础镜像的容器,进入容器内部安装依赖、写代码、调试。 特点: 开发效率低|调试困难|环境容易丢失|依赖管理混乱 方式二:本地开发+docker打包部署 操作:在本地python环境进行开发,开发完成后通过Dockerfile构建镜像生产镜像。 特点: 开发体验好|环境隔离|可复现性强|镜像精简 开发案例方案一 实验环境 |macOS|Docker version 28.0.1, build 068a01e`` 12345678910111213141516171819202122232425262728293031# 终端命令步骤# 拉取基础镜像docker pull python:3.11-slim-bullseye# 新建容器...
service_manager
1. 程序整体架构分析核心设计模式:单例模式 + 命令模式123456789101112131415161718service_manager.py├── 配置层 (Configuration Layer)│ ├── 服务定义 (services字典)│ ├── 环境配置 (conda环境路径)│ └── 日志配置 (logging配置)├── 管理层 (Management Layer)│ ├── ServiceManager类│ ├── 进程管理 (PID文件持久化)│ └── 状态监控 (进程状态检查)├── 操作层 (Operation Layer)│ ├── 启动服务 (start_service)│ ├── 停止服务 (stop_service)│ ├── 重启服务 (restart_service)│ └── 状态查看 (status)└── 接口层 (Interface Layer) ├── 命令行参数解析 ├── 信号处理 └── 用户交互 2. 核心组件详解2.1 配置层设计12345678910#...
机器学习之集成学习
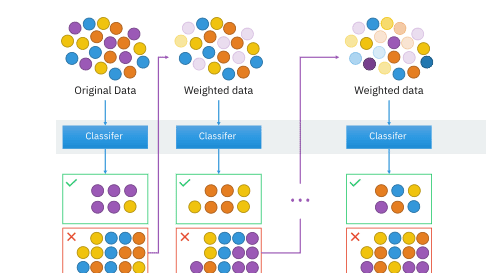
机器学习之集成学习概述集成学习(Ensemble Learning)是机器学习中一种重要的方法,它通过组合多个基础学习器来构建一个更强大的学习器。这种方法的核心思想是”三个臭皮匠,胜过一个诸葛亮”,通过多个模型的集体智慧来提高预测的准确性和稳定性。 集成学习的基本概念什么是集成学习?集成学习是一种机器学习范式,它通过构建并结合多个学习器来完成学习任务。这些学习器可以是同类型的(如多个决策树),也可以是不同类型的(如决策树、神经网络、支持向量机等)。 集成学习的优势 提高预测准确性:多个模型的组合通常比单个模型表现更好 增强泛化能力:减少过拟合风险,提高模型对新数据的适应能力 提高稳定性:降低单个模型的不稳定性影响 处理复杂问题:能够处理单个模型难以解决的复杂问题 主要的集成方法1. Bagging(Bootstrap...
机器学习之SVM
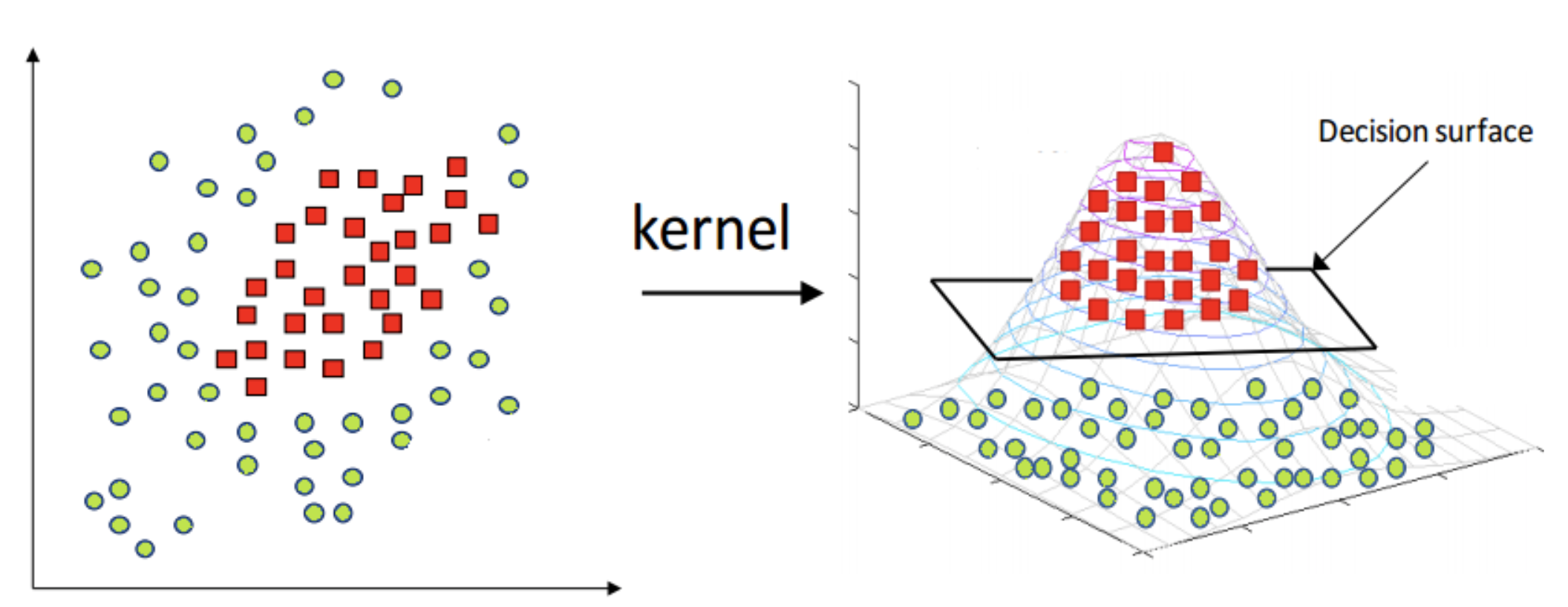
支持向量机 (SVM) - 机器学习中的强大分类器什么是SVM?支持向量机(Support Vector Machine, SVM)是一种强大的监督学习算法,主要用于分类问题,也可以用于回归分析。它的核心思想是找到一个最优的超平面来分隔不同类别的数据。 核心概念1. 支持向量 (Support Vectors)支持向量是数据集中位置特殊的关键点,它们决定了分类超平面的位置。这些点距离分类边界最近,对模型的性能起着决定性作用。 2. 最大间隔 (Maximum Margin)SVM的核心目标是找到能够最大化分类间隔的超平面,这样可以提高模型的泛化能力。 3. 分隔超平面 (Separating Hyperplane) 对于线性可分数据,可以通过一条直线(二维)或超平面(高维)将不同类别的数据完全分开 这条分隔线称为分隔超平面 数学原理拉格朗日乘子法SVM通过拉格朗日乘子法 (Method of Lagrange Multiplier)...
机器学习之回归
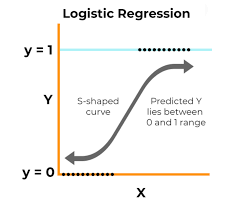
Logistic回归Logistic回归是一种用于二分类问题的统计学习方法。它通过对输入特征的线性组合结果应用Sigmoid函数,将输出映射到0和1之间,从而预测某个事件发生的概率。与线性回归不同,逻辑回归的输出是概率值,常用于分类任务。 基础概念Sigmoid函数Sigmoid函数是一种常用的激活函数,定义为: $$\sigma(z) = \frac{1}{1 + e^{-z}}$$ 它的输出范围在0到1之间,适合用于概率预测。 单位阶跃函数与Sigmoid函数在二分类问题中,我们希望模型能够根据输入预测类别(0或1)。理想情况下,可以使用单位阶跃函数(Heaviside step function)来实现: $$f(x) = \begin{cases}1, & x \geq 0 \0, & x <...
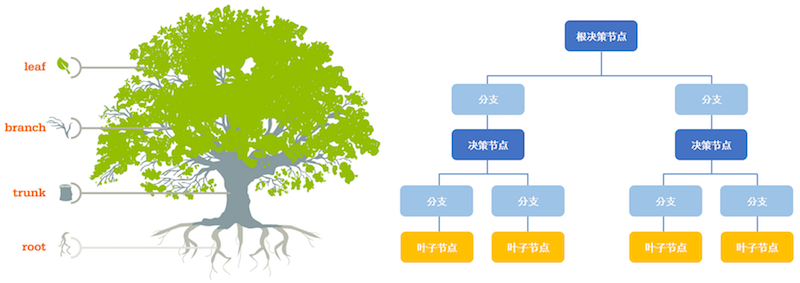
机器学习之决策树详解:从原理到实践
引言决策树(Decision Tree)是机器学习中最基础且最实用的算法之一,广泛应用于分类和回归问题。它以其直观的树形结构、易于理解和解释的特点,成为数据挖掘和机器学习领域的经典算法。 什么是决策树?决策树是一种树形结构的预测模型,通过一系列的问题(特征判断)来对数据进行分类或预测。每个内部节点代表一个特征测试,每个分支代表测试的一个可能结果,每个叶节点代表一个预测结果。 决策树的基本结构12345根节点 (Root Node) → 特征判断 ├── 分支1 → 内部节点 → 特征判断 │ ├── 分支1.1 → 叶节点 (预测结果1) │ └── 分支1.2 → 叶节点 (预测结果2) └── 分支2 → 叶节点 (预测结果3) 核心概念详解1. 信息熵 (Information Entropy)信息熵是衡量数据集不确定性的重要指标,由香农(Shannon)提出。 定义: 对于数据集D,其熵定义为: 1H(D) = -Σ(pi *...
机器学习之朴素贝叶斯详解
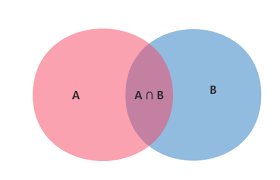
目录 朴素贝叶斯概述 数学基础 朴素贝叶斯分类器 实际应用 优缺点分析 总结 朴素贝叶斯概述朴素贝叶斯(Naive Bayes)是一种基于贝叶斯定理的概率分类算法,属于监督学习中的生成模型。它以其简单、高效和在某些场景下的优秀表现而闻名。 核心思想朴素贝叶斯的核心假设是特征条件独立性,即假设所有特征之间相互独立。虽然这个假设在现实中往往不成立,但正是这种”朴素”的假设使得算法计算简单且效果良好。 分类原理利用贝叶斯公式根据特征的先验概率计算出其后验概率,然后选择具有最大后验概率的类作为该特征所属的类: $$P(C|X) = \frac{P(X|C) \cdot P(C)}{P(X)}$$ 其中: $P(C|X)$ 是后验概率 $P(X|C)$ 是似然概率 $P(C)$ 是先验概率 $P(X)$ 是证据因子 数学基础条件概率条件概率是指在事件B发生的情况下,事件A发生的概率,记作 $P(A|B)$: $$P(A|B) = \frac{P(A \cap B)}{P(B)}$$ 全概率公式如果事件 $A_1, A_2, …, A_n$...
机器学习之KNN算法详解
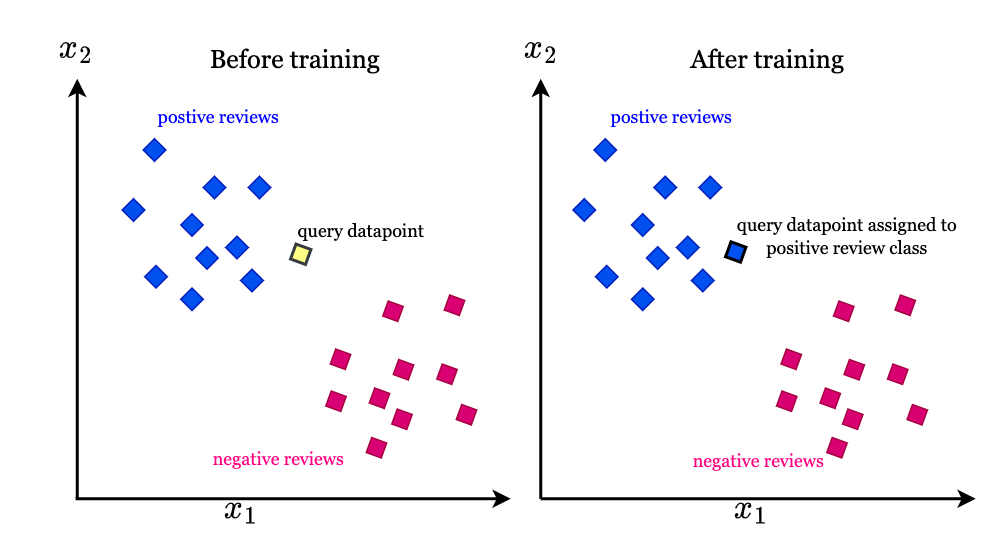
什么是K-近邻算法?K-近邻(K-Nearest Neighbor, KNN)是一种监督学习算法,属于基于实例的学习或懒惰学习方法。它的核心思想是:物以类聚,即相似的对象应该属于同一类别。 算法基本概念 输入:样本的特征向量(在特征空间中的点) 输出:样本的类别标签 核心假设:相似的样本具有相似的标签 KNN算法原理详解1. 训练阶段KNN算法实际上没有显式的训练过程,它只是将训练数据存储起来,因此被称为”懒惰学习”。 2. 预测阶段当需要对新样本进行分类时,算法执行以下步骤: 距离计算:计算新样本与所有训练样本之间的距离 排序:将所有距离按从小到大排序 投票:选择前K个最近邻的类别标签 决策:通过多数投票确定新样本的类别 距离度量方法欧几里得距离(Euclidean Distance)最常用的距离度量方法,适用于连续型特征: $$d(x, y) = \sqrt{\sum_{i=1}^{n}(x_i - y_i)^2}$$ 曼哈顿距离(Manhattan Distance)适用于离散型特征或城市街区距离: $$d(x, y) =...