机器学习
(注:博客属个人复习笔记,不会介绍基础概念,仅记录个人遗忘的部分知识点)
机器学习 概述
- “机器学习是对能通过经验自动改进的计算机算法的研究”
- “机器学习是用数据或以往的经验,以此优化计算机程序的性能标准”
- 机器学习和深度学习的最大区别在神经网络,深度学习使用神经网络去提取事物的深层或者说是隐性的一些特征
常见的模型指标
- 正确率 —— 提取出的正确信息条数 / 提取出的信息条数
- 召回率 —— 提取出的正确信息条数 / 样本中的信息条数
- F 值 —— 正确率 * 召回率 * 2 / (正确率 + 召回率)(F值即为正确率和召回率的调和平均值)
特征工程 (Feature Engineering)
特征工程是机器学习项目中最关键的环节,直接影响模型性能。好的特征工程可以显著提升模型效果。
特征工程概述
- 定义:从原始数据中提取、转换、选择对模型有用的特征
- 重要性:数据和特征决定了机器学习的上限,模型和算法只是逼近这个上限
- 目标:提高模型性能、降低计算复杂度、增强模型可解释性
特征选择 (Feature Selection)
定义:从M个特征中选择N个最有效特征,降低数据维度,提高算法性能
特征选择方法
Filter方法:基于统计指标筛选
- 相关系数:皮尔逊相关系数、斯皮尔曼相关系数
- 卡方检验:检验特征与目标变量的独立性
- 互信息:衡量特征与目标变量的相互依赖程度
- 方差分析:选择方差较大的特征
- F检验:检验特征对目标变量的显著性
Wrapper方法:基于模型性能选择
- 前向选择:逐步添加特征
- 后向消除:逐步删除特征
- **递归特征消除(RFE)**:基于模型权重排序
- **遗传算法(GA)**:模拟自然选择
- **模拟退火(SA)**:避免局部最优
Embedded方法:模型内置特征选择
- **L1正则化(Lasso)**:产生稀疏解,自动特征选择
- **L2正则化(Ridge)**:缩小特征权重
- Elastic Net:L1+L2正则化
- 决策树:基于信息增益/基尼指数
- 随机森林:基于特征重要性
特征提取 (Feature Extraction)
定义:将原始特征转换为新的特征表示,保留重要信息
降维技术
主成分分析(PCA)
- 线性降维,最大化方差
- 正交变换,消除特征间相关性
- 应用:图像压缩、数据可视化
线性判别分析(LDA)
- 有监督降维,最大化类间距离,最小化类内距离
- 最多降至(类别数-1)维
- 应用:人脸识别、文本分类
t-SNE
- 非线性降维,保持局部结构
- 适合高维数据可视化
- 应用:数据探索、聚类可视化
自编码器(Autoencoder)
- 神经网络降维,学习非线性映射
- 编码器压缩,解码器重构
- 应用:图像压缩、异常检测
特征预处理
数据清洗
- 异常值检测:
- 3σ原则:超出均值±3倍标准差
- IQR方法:Q1-1.5×IQR ~ Q3+1.5×IQR
- 孤立森林:基于异常分数
- 缺失值处理:
- 删除:样本少时可用
- 填充:均值、中位数、众数
- 插值:线性插值、样条插值
- 预测:用其他特征预测缺失值
数据变换
标准化/归一化
- 标准化:(x - μ) / σ,均值为0,标准差为1
- 归一化:(x - min) / (max - min),缩放到[0,1]
- 鲁棒缩放:(x - Q2) / (Q3 - Q1),基于分位数
非线性变换
- 对数变换:log(x),处理右偏分布
- 指数变换:exp(x),处理左偏分布
- Box-Cox变换:λ参数优化,使分布更接近正态
- 幂变换:x^p,调整分布形状
离散化
- 等宽分箱:按数值范围等分
- 等频分箱:按样本数量等分
- 聚类分箱:基于聚类结果分箱
- 决策树分箱:基于目标变量最优分割
编码技术
类别特征编码
- One-Hot编码:每个类别一个特征
- Label编码:类别映射为整数
- Target编码:用目标变量均值编码
- Hash编码:减少维度,处理高基数特征
时间特征处理
- 周期性编码:sin(2π×t/T)、cos(2π×t/T)
- 时间窗口特征:滑动平均、滑动标准差
- 滞后特征:t-1、t-2时刻的值
特征构建
交互特征
- 多项式特征:x₁²、x₁x₂、x₂²
- 统计特征:均值、方差、最大值、最小值
- 比率特征:x₁/x₂、x₁-x₂
- 组合特征:基于业务逻辑的特征组合
聚合特征
- 时间聚合:日、周、月、季度统计
- 空间聚合:地理区域、用户群体统计
- 序列聚合:滑动窗口、指数平滑
特征监控
特征质量监控
- 覆盖率:非空值比例
- 准确率:数据质量评估
- 稳定性:特征分布变化
- 相关性:特征间相关性变化
特征漂移检测
- 统计检验:KS检验、卡方检验
- 分布距离:KL散度、JS散度
- 模型性能:特征重要性变化
- 业务指标:业务KPI变化
特征工程最佳实践
- 业务理解优先:基于领域知识构建特征
- 数据探索:充分了解数据分布和关系
- 迭代优化:特征工程是迭代过程
- 验证效果:交叉验证评估特征效果
- 文档记录:记录特征含义和构建逻辑
- 版本控制:特征工程代码版本管理
- 自动化:构建特征工程流水线
- 监控告警:实时监控特征质量
常见陷阱
- 数据泄露:使用未来信息
- 过拟合:特征过多导致过拟合
- 维度诅咒:高维空间稀疏性
- 特征冗余:高度相关特征
- 分布偏移:训练测试分布不一致
监督学习
- 有标签
KNN (K-Nearest Neighbor)
- 核心思想:物以类聚,近邻样本属于同一类别的概率较大
- 算法步骤:
- 计算待分类样本与训练集中所有样本的距离
- 按距离递增排序,选取前K个最近邻
- 统计K个最近邻中各类别的频数
- 返回频数最高的类别作为预测结果
- 距离度量:
- 欧几里得距离:√[(x₁-y₁)² + (x₂-y₂)² + … + (xₙ-yₙ)²]
- 曼哈顿距离:|x₁-y₁| + |x₂-y₂| + … + |xₙ-yₙ|
- 闵可夫斯基距离:(∑|xᵢ-yᵢ|ᵖ)^(1/p)
- K值选择:通常取奇数,避免平票;K太小容易过拟合,K太大容易欠拟合
- 优缺点:
- 优点:简单易理解,无需训练过程,对异常值不敏感
- 缺点:计算复杂度高,对内存要求大,需要特征标准化
线性回归 (Linear Regression)
- 核心思想:用线性函数拟合数据,最小化预测值与真实值的平方差
- 数学表达:y = w₁x₁ + w₂x₂ + … + wₙxₙ + b
- 损失函数:均方误差 MSE = (1/n)∑(yᵢ - ŷᵢ)²
- 求解方法:
- 最小二乘法:w = (X^T X)^(-1) X^T y
- 梯度下降:w = w - α∇J(w)
- 评估指标:R²、均方根误差(RMSE)、平均绝对误差(MAE)
- 假设条件:
- 线性关系
- 独立性
- 同方差性
- 正态分布残差
朴素贝叶斯算法 (Naive Bayes)
- 核心思想:基于贝叶斯定理,假设特征之间相互独立
- 贝叶斯定理:P(A|B) = P(B|A) × P(A) / P(B)
- 分类公式:P(y|x) ∝ P(y) × ∏P(xᵢ|y)
- 三种模型:
- 高斯朴素贝叶斯:连续特征,假设服从正态分布
- 多项式朴素贝叶斯:离散特征,文本分类常用
- 伯努利朴素贝叶斯:二值特征
- 拉普拉斯平滑:P(xᵢ|y) = (Nᵢ + α) / (N + α×k)
- 优缺点:
- 优点:训练速度快,对小数据集效果好,处理多分类问题
- 缺点:特征独立性假设过强,对数据分布敏感
局部加权线性回归 (Locally Weighted Linear Regression)
- 核心思想:对每个预测点,根据距离赋予不同权重,近邻点权重更大
- 权重函数:w(i) = exp(-(x^(i) - x)² / (2τ²))
- 参数τ:带宽参数,控制权重衰减速度
- 特点:非参数方法,计算复杂度高,需要存储所有训练数据
支持向量机 (Support Vector Machine)
- 核心思想:寻找最优超平面,最大化两类样本的间隔
- 数学表达:w^T x + b = 0,其中|w^T x + b| / ||w||为点到超平面的距离
- 优化目标:min (1/2)||w||²,s.t. yᵢ(w^T xᵢ + b) ≥ 1
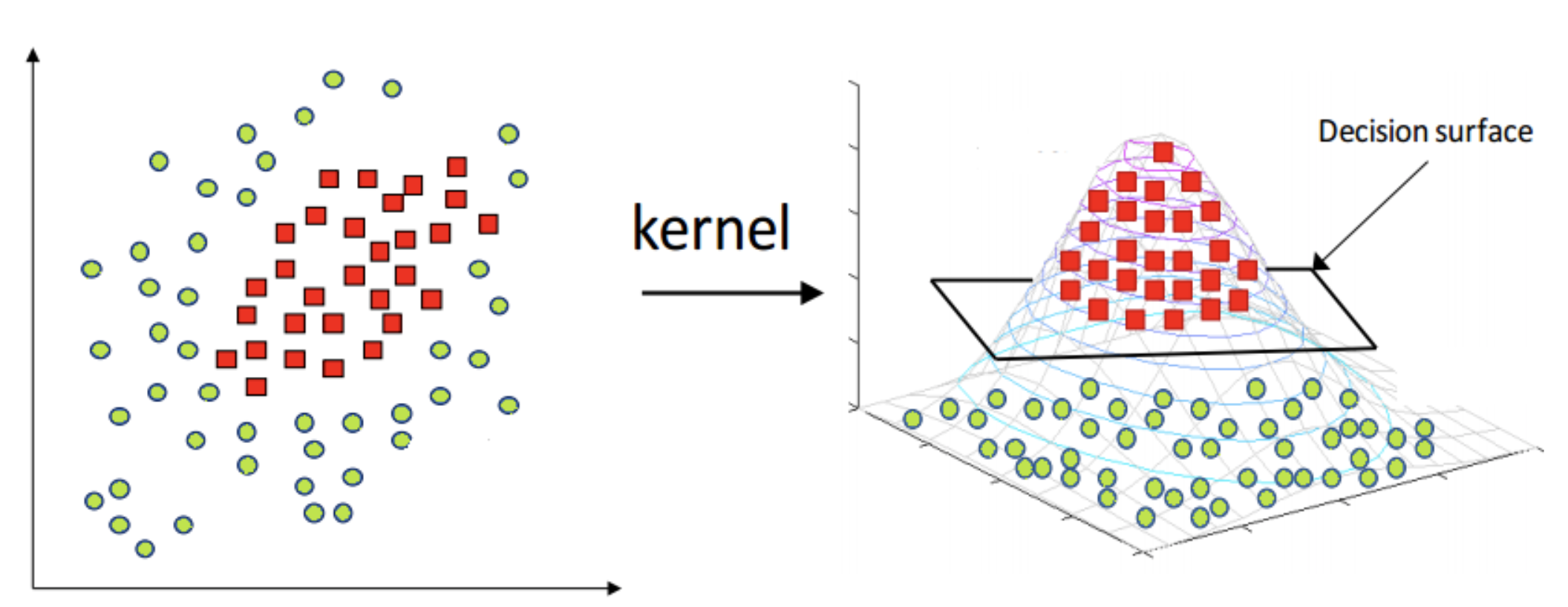
- 核函数:
- 线性核:K(x,y) = x^T y
- 多项式核:K(x,y) = (γx^T y + r)^d
- RBF核:K(x,y) = exp(-γ||x-y||²)
- Sigmoid核:K(x,y) = tanh(γx^T y + r)
- 软间隔:引入松弛变量ξ,允许部分样本分类错误
- 优缺点:
- 优点:泛化能力强,适合高维数据,核函数灵活
- 缺点:对大规模数据训练慢,参数调优复杂
Ridge回归 (岭回归)
- 核心思想:在线性回归基础上添加L2正则化项,防止过拟合
- 损失函数:J(w) = ||y - Xw||² + λ||w||²
- 求解:w = (X^T X + λI)^(-1) X^T y
- 参数λ:正则化强度,λ越大,模型越简单
- 特点:处理多重共线性问题,所有特征权重都会缩小但不会为零
决策树 (Decision Tree)
- 核心思想:通过特征分割构建树形结构,每个节点代表一个特征判断
- 分割准则:
- 信息增益:IG(D,A) = H(D) - H(D|A)
- 信息增益比:IGR(D,A) = IG(D,A) / H(A)
- 基尼指数:Gini(D) = 1 - ∑pᵢ²
- 停止条件:
- 节点样本数小于阈值
- 节点深度达到最大值
- 所有样本属于同一类
- 剪枝:
- 预剪枝:在生长过程中停止
- 后剪枝:先生长后剪枝(CART算法)
- 优缺点:
- 优点:可解释性强,能处理数值和类别特征
- 缺点:容易过拟合,对数据变化敏感
最小回归系数估计 (Least Absolute Shrinkage and Selection Operator, LASSO)
- 核心思想:在线性回归基础上添加L1正则化项,产生稀疏解
- 损失函数:J(w) = ||y - Xw||² + λ||w||₁
- 特点:
- 自动特征选择,部分特征权重变为零
- 处理多重共线性
- 适合高维稀疏数据
- 求解方法:坐标下降法、最小角回归(LARS)
无监督学习
- 无标签
K-均值 (K-Means)
- 核心思想:将数据划分为K个簇,每个簇的中心代表该簇
- 算法步骤:
- 随机选择K个初始中心点
- 将每个样本分配到最近的中心点
- 重新计算每个簇的中心点
- 重复步骤2-3直到收敛
- 目标函数:最小化簇内平方误差 SSE = ∑∑||x - μᵢ||²
- 初始化方法:
- 随机初始化
- K-means++:选择距离已选中心点较远的点
- 优缺点:
- 优点:简单高效,适合大规模数据
- 缺点:需要预先指定K值,对初始中心敏感,只能发现球形簇
最大期望算法 (Expectation-Maximization, EM)
- 核心思想:通过迭代优化求解含有隐变量的概率模型参数
- 算法步骤:
- E步:计算隐变量的期望
- M步:最大化期望似然函数
- 应用场景:
- 高斯混合模型(GMM)
- 隐马尔可夫模型(HMM)
- 主题模型(LDA)
- 收敛性:保证收敛到局部最优解
马尔可夫决策过程 (Markov Decision Process, MDP)
- 核心思想:用五元组(S,A,P,R,γ)描述强化学习问题
- S:状态空间
- A:动作空间
- P:状态转移概率
- R:奖励函数
- γ:折扣因子
- 价值函数:V(s) = E[∑γᵗRₜ₊₁|S₀=s]
- 策略:π(a|s)表示在状态s下选择动作a的概率
- 最优策略:π*(s) = argmax Q*(s,a)
- 求解方法:
- 值迭代:V(s) = max∑P(s’|s,a)[R(s,a,s’) + γV(s’)]
- 策略迭代:交替进行策略评估和策略改进
- 应用:机器人控制、游戏AI、推荐系统
模型评估与选择
交叉验证
- K折交叉验证:将数据分为K份,每次用K-1份训练,1份验证
- **留一法(LOOCV)**:K=N的特殊情况
- 分层K折:保持各类别比例一致
过拟合与欠拟合
- 过拟合:模型在训练集表现好,测试集表现差
- 解决方法:正则化、增加数据、简化模型、集成学习
- 欠拟合:模型在训练集和测试集表现都差
- 解决方法:增加模型复杂度、减少正则化、特征工程
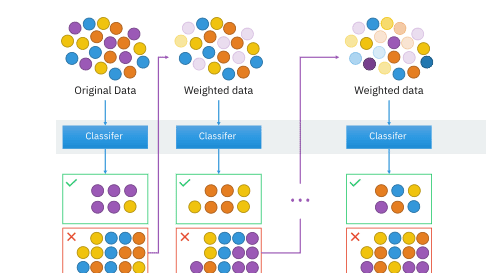
集成学习
- Bagging:并行训练多个模型,投票或平均
- 随机森林:决策树的Bagging
- Boosting:串行训练,每个模型关注前一个模型的错误
- AdaBoost:调整样本权重
- GBDT:梯度提升决策树
- XGBoost:优化的GBDT实现
- Stacking:用元学习器组合多个基学习器
深度学习基础
神经网络
- 前馈神经网络:信息单向传播
- 激活函数:
- ReLU:max(0,x),解决梯度消失
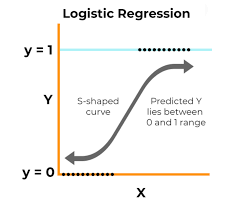
- Sigmoid:1/(1+e^(-x)),输出概率
- Tanh:tanh(x),输出[-1,1]
- 反向传播:链式法则计算梯度
卷积神经网络(CNN)
- 卷积层:提取局部特征
- 池化层:降维,提高鲁棒性
- 全连接层:分类决策
循环神经网络(RNN)
- LSTM:长短期记忆网络,解决梯度消失
- GRU:门控循环单元,简化版LSTM
- 应用:序列建模、自然语言处理
实践要点
数据预处理
- 标准化:(x - μ) / σ
- 归一化:(x - min) / (max - min)
- 缺失值处理:删除、填充、插值
特征选择
- 过滤法:基于统计指标
- 包装法:基于模型性能
- 嵌入法:模型内置选择
超参数调优
- 网格搜索:穷举搜索
- 随机搜索:随机采样
- 贝叶斯优化:基于概率模型
模型部署
- 模型保存:pickle、joblib、ONNX
- API设计:RESTful、gRPC
- 监控:性能指标、数据漂移检测
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 廾匸!